Greene Lab, Department of Systems Pharmacology and Translational Therapeutics, University of Pennsylvania
This report is available online at https://doi.org/10.6084/m9.figshare.5346577.
This manuscript was automatically generated from zietzm/Vagelos2017@e4482aa on August 25, 2017.
Drug development times and R&D expenditures have risen considerably in the last decades. In fact, to bring a new compound to market can take 14 years on average [1]. This development process, according to a 2016 estimate by DiMasi et al. [2], costs an average of $2.87 billion dollars, including post-approval R&D. This amount is up from two previous studies by the same authors which found the average captialized R&D costs (in inflation-adjusted 2016 dollars) to be $1.06 billion in 2003 [3] and $568 million in 1991 [4]. Despite increases in drug development time and expenditures, the rate of R&D failure has increased since the 1990s [5]. Only about one in 5,000 compounds which begin preclinical testing are eventually approved [6]. Even among those which enter phase I of clinical development, only an estimated one in ten drugs will receive FDA approval [7].
Drug repurposing refers to the application of an existing therapeutic to a different disease than the one for which it was originally intended. Because candidates for drug repurposing have already been approved for other diseases, the time and cost associated with repurposing a drug are very small compared to the development of a new drug [8]. In fact, even compounds which have been deemed safe but have failed in clinical development for other reasons can be candidates for drug repurposing. Several examples exist of drugs which have been repurposed, for example aspirin to treat coronary artery disease, sildenafil to treat erectile dysfunction, and gabapentin to treat postherpetic neuralgia. Most successfully repurposed drugs were discovered serendipitously and not through any systematic discovery mechanism. Our goal is to make accurate predictions of drugs which are candidates for drug repurposing. We hope to do this using heterogeneous networks of biomedical information to learn the patterns of connections between compounds which treat diseases.
This summer I worked within the Greene Lab project called ‘Hetmech’ [9]. Hetmech aims to improve upon and expand our existing method for predicting drug repurposing targets.
I had three primary aims for my work this summer. The details of each are covered in the Methods section.
First, I wanted to add a capability within Hetmech to compute precisely the degree-weighted path count (DWPC). Previously, the three options had been an extremely slow DWPC method, an inaccurate DWPC method, and a degree-weighted walk count (DWWC), whose limitations will be covered in the Methods section.
Second, I hoped to decrease the time required to make calculations of DWPC. Towards this aim, I hoped to speed up computation by at least an order of magnitude. Sparse matrices and parallel computation were planned solutions to this problem.
Finally, it was my goal to add a multiple search capability. This involves querying a set of nodes to return a set of predictions for nodes which connect the queried nodes. For example, one should be able to search a set of symptoms and return a list of potential diseases that connect the symptoms. As with the previous problems, moving to strictly matrix computation makes this much more simple.
My secondary aim for the summer was to become familiar with and contribute to open-source, reproducible, computational science in biology. I hoped to contribute to a collaboratively written review of deep learning methods in the fields of biology and medicine [10].
Heterogeneous networks (‘hetnets’) are networks with multiple node types and edge types. In the network used this summer, titled Hetionet v1.0 (Figure 1B), nodes represent instances of 11 biomedical entity types, and edges correspond to one of 24 edge types, or relationships between entities. ‘Graph’ in this context refers to the entire network of nodes and edges. We define ‘metagraph’ to mean a graph of the types of nodes and edges in Hetionet (Figure 1A).
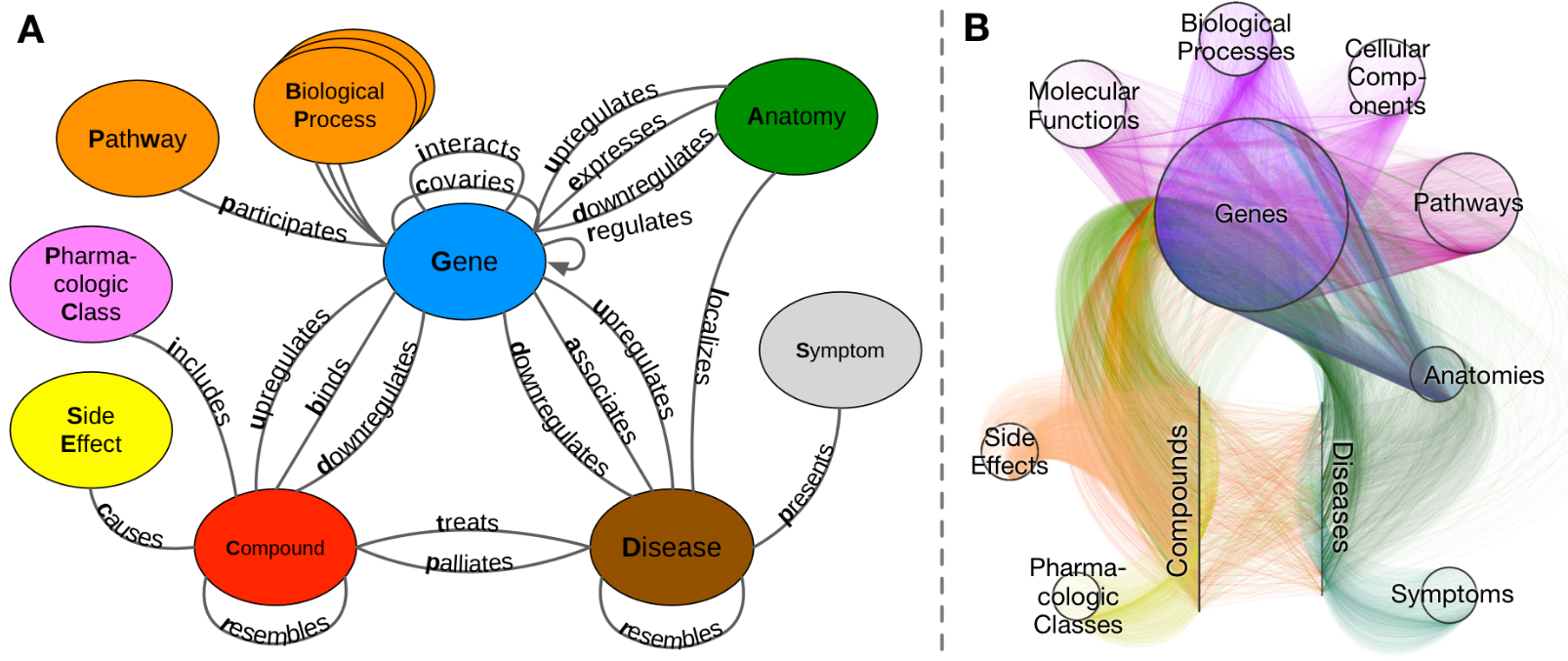
Figure 1: A. Metagraph. The graph of metandoes (node types) and metaedges (edge types). B. Graph (Hetionet v1.0) The circles and lines represent nodes within the labeled types. For example, within the metanode ‘Anatomy’ we could have the node ‘Leukocyte’.
Hetionet v1.0 incorporated 47,031 nodes and 2,250,197 edges [11]. A further breakdown of the nodes and edges can be found below in Tables 1 and 2, respectively.
| Metanode | Nodes |
|---|---|
| Anatomy | 402 |
| Biological Process | 11,381 |
| Cellular Component | 1,391 |
| Compound | 1,552 |
| Disease | 137 |
| Gene | 20,945 |
| Molecular Function | 2,884 |
| Pathway | 1,822 |
| Pharmacologic Class | 345 |
| Side Effect | 5,734 |
| Symptom | 438 |
| Metaedge | Edges | Source |
|---|---|---|
| Anatomy-downregulates-Gene | 102,240 | Bgee |
| Anatomy-expresses-Gene | 526,407 | Bgee and TISSUES |
| Anatomy-upregulates-Gene | 97,848 | Bgee |
| Compound-binds-Gene | 11,571 | BindingDB, DrugBank, DrugCentral |
| Compound-causes-Side Effect | 138,944 | SIDER |
| Compound-downregulates-Gene | 21,102 | LINCS L1000 |
| Compound-palliates-Disease | 390 | PharmacotherapyDB |
| Compound-resembles-Compound | 6,486 | Dice coefficient = 0.5 |
| Compound-treats-Disease | 755 | PharmacotherapyDB |
| Compound-upregulates-Gene | 18,756 | LINCS L1000 |
| Disease-associates-Gene | 12,623 | GWAS Catalog, DISEASES, DisGeNET, DOAF |
| Disease-downregulates-Gene | 7,623 | STARGEO |
| Disease-localizes-Anatomy | 3,602 | MEDLINE |
| Disease-presents-Symptom | 3,357 | MEDLINE |
| Disease-resembles-Disease | 543 | MEDLINE |
| Disease-upregulates-Gene | 7,731 | STARGEO |
| Gene-covaries-Gene | 61,690 | Evolutionary rate covariation = 0.75 |
| Gene-interacts-Gene | 147,164 | Evolutionary rate covariation = 0.75 |
| Gene-participates-Biological Process | 559,504 | Gene Ontology |
| Gene-participates-Cellular Component | 73,566 | Gene Ontology |
| Gene-participates-Molecular Function | 97,222 | Gene Ontology |
| Gene-participates-Pathway | 84,372 | Gene Ontology |
| Gene-regulates-Gene | 265,672 | Gene Ontology |
| Pharmacologic Class-includes-Compound | 1,029 | DrugCentral |
An adjacency matrix refers to a labeled matrix with 1 or 0 at every position, corresponding to the presence or absence of a connection between two nodes [12]. The matrix is labeled, meaning that each row and column correspond to a source and target node, respectively. A function was created, titled metaedge_to_adjacency_matrix which performed the conversion from a string metaedge, such as ‘DaG’, to an adjacency matrix.
Figure 2: An example graph. Blue nodes are genes, while green nodes are diseases. The edge type between all the nodes in this graph is ‘DaG’ or ‘Disease-associates-Gene’. This is also the complete graph for the relationship ‘DaGaD’ starting with ‘spinal cancer’.
For example, the graph in Figure 2 has the following adjacency matrix corresponding to ‘GaD’:
\[ \begin{equation} \begin{bmatrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 \end{bmatrix} \end{equation} \]
with labels for rows and columns, respectively:
\[\begin{bmatrix} \textrm{NF2}\\ \textrm{NRXN2}\\ \textrm{SMARCE1} \end{bmatrix}\] \[\begin{bmatrix} \textrm{epilepsy syndrome}\\ \textrm{kidney cancer}\\ \textrm{pancreatic cancer}\\ \textrm{spinal cancer}\\ \textrm{malignant mesothelioma}\\ \textrm{peripheral nervous system neoplasm}\\ \textrm{autistic disorder}\\ \textrm{meningioma}\\ \textrm{salivary gland cancer} \end{bmatrix}\]An adjacency matrix is identical to the information about connections between nodes along a given metaedge. Another way to consider an adjacency matrix is as a list of the nodes at which one can arrive in one step from a given start node. In this sense, performing a matrix multiplication with two adjacency matrices gives the nodes at which one can arrive in exactly two steps. Further, an arbitrary number of multiplications can be performed between adjacency matrices corresponding to various metaedges, so long as the dimensionality is appropriate to the matrix multiplication in question. Using this method, we can extract what is known as a walk count, or the number of ways to traverse the graph between two nodes. In this way of thinking, an adjacency matrix corresponds to the path count for paths of length one. Using the graph in Figure 2, we could perform a traversal along the metapath ‘GaDaG’, and would obtain the following matrix:
\[\begin{bmatrix} 6 & 1 & 2\\ 1 & 3 & 1\\ 2 & 1 & 3 \end{bmatrix}\]Notice that the elements along the main diagonal of the above matrix are not zero. This indicates that we are accounting for walks in which we traverse the nodes as follows: ‘NF2’ ⟶ ‘kidney cancer’ ⟶ ‘NF2’. Looping walks do not provide useful information, and they introduce considerable noise in measures of connection between nodes. We therefore wanted to eliminate any usage of walk count and replace it with path count, where a path is a type of walk which cannot loop backwards on itself. In this example and for paths of length two, this is trivial; we simply subtract the main diagonal, and we have converted from a walk count to a path count. However, this conversion becomes non-trivial when dealing with longer paths and overlapping metanode repeats. Using the graph in Figure 2, NF2—associates—spinal cancer—resembles—peripheral nervous system neoplasm—associates—NF2 is considered a walk, but it is not a path because its start and end nodes are the same. Note that it is perfectly acceptable to repeat metanodes, meaning that we can have metapaths of the form ‘CrCrCrC’. Paths simply exclude the repeat of specific nodes within an ordering of nodes.
Path counts provide useful information for predicting potential new relationships within a graph. Higher path-counts between two nodes shows good performance as a feature for predicting novel connections [13]. However, as high-degree nodes by definition make many connections, superior performance was achieved by downweighting nodes according to their degree. To do this, row sums and column sums are taken for a matrix at each step. These one-dimensional arrays are exponentiated by a damping exponent, and the matrix is multiplied by each array (vector). This represents the ‘degree-weight’ portion of the ‘degree-weighted path count’. My work toward this will be further discussed in the Results section.
Once we have calculated the DWPC over all the considered metapaths, we use the best of these path counts as features to train a machine learning (logistic regression) model. Once trained, the model’s performance is assessed by comparing its predictions to known relationships. Since we cannot exclude test paths from the overall network, however, we must compare each feature’s performance to its performance on a ‘permuted hetnet’, or an identical network in which the edges have been randomly reassigned, while node-degree has been universally preserved. The corrected measure we use to assess feature performance is therefore the ΔAUROC, the difference in area under (AU) the receiver operating characteristic (ROC) curve. Once our model is trained and tested, we can translate DWPC data for specific connections into the probability that a compound treats a disease.
All computational work was done in Python version 3.6. We used an open-source Conda environment to manage packages and dependencies for Python.
Python’s mathematical and array library, NumPy [14], has an n-dimensional array class called an ndarray. numpy.ndarrays are very useful for representing matrix information, and have superior functionality for our purposes than the native numpy.matrix class. However, as can be seen in Table 1, the number of nodes in a given adjacency matrix can be upwards of 20,000. In performing matrix multiplications, this can become a computation-intensive process that requires both significant CPU power and memory. Additionally, since the adjacency matrices are full of more zeros than ones, a majority of the multiplications performed are trivial zero multiplications.
One of my early goals for the summer was the conversion of all walk-count (and subsequently, path count) functions to sparse matrices. Sparse matrices, as employed by the Python library SciPy [15], represent data in matrices which are primarily composed of zeros. The selection of sparse representation and threshold are discussed in the Results section, but sparse matrices warrant a brief description.
In the sparse representation we used, compressed-sparse-column format (CSC), a matrix is stored as three one-dimensional arrays.
Consider the following matrix:
\[\begin{bmatrix} 4 & 5 & 0 & 0\\ 0 & 0 & 1 & 0\\ 3 & 0 & 0 & 9\\ 0 & 6 & 0 & 5 \end{bmatrix}\]We represent the nonzero elements with one array, with the elements being taken from top to bottom, from left to right.
\[\begin{bmatrix} 4 & 3 & 5 & 6 & 1 & 9 & 5 \end{bmatrix}\]Next, we give the row indices of these elements.
\[\begin{bmatrix} 0 & 2 & 0 & 3 & 1 & 2 & 3 \end{bmatrix}\]The final array represents what is called a column pointer. This array gives the indices of the first array where each column starts.
\[\begin{bmatrix} 0 & 2 & 4 & 5 & 7 \end{bmatrix}\]These three arrays represent the entirety of a matrix.
A significant amount of work done later in the summer involved attempting to compare the new functions to the quite slow old functions. As has become relatively standard for much of computational work, we made use of Jupyter notebooks [16] to display the code used to run analysis and its output in a re-usable way. Within this, we were able to effectively incorporate the data manipulation and analysis library pandas [17] and the multiprocessing library concurrent.futures [18]. For visualization, we utilized the online service Neo4j to represent Hetionet v1.0 [19], and the Python graphing libraries Matplotlib [20] and seaborn [21].
The most important tool we used this summer to track progress was the version control software, Git. Our repositories were hosted on the online git hosting service, GitHub [22]. Specifically, every contribution I made this summer can be viewed in detail at my GitHub profile (https://git.io/v5qC9). This will be discussed further in the Results section below.
The main problem towards which I worked this summer was an implementation of the degree-weighted path count. While the degree-weighted walk count is relatively trivial to implement with matrix multiplication, the path count is non-trivial. If computational efficiency is to be considered, each category of metapath will require a different path-count method. As of mid-August 2017, I have merged 7 pull requests into the main Hetmech repository on GitHub, and I have one open development branch. These contributions amounted to 1043 lines added and 264 lines deleted in the repository.
I have completed an implementation of the degree-weighted path count (DWPC) in the form of several independent functions. What follows are the specifics of this new method.
When a user calls the dwpc function over a metapath, a series of steps occur before any actual path-counting occurs. First, the metapath is categorized according to its repeated metanodes. For example, the metapath ‘GaDrDaG’, (‘Gene-associates-Disease-resembles-Disease-associates-Gene’) would be classified BAAB. Further examples of this classification method are in Table 3 below.
Next, the metapath is split into segments according to its classification. This step allowed for the abstraction of metapath patterns to metapaths which followed the pattern of a classification but included randomly inserted, non-repeating metanodes anywhere in the bath. Splitting the metapath essentially allowed us to work with paths like A-B-C-D-B-A in the same way that we work with A-B-B-A, by abstracting any non-repeating metanodes to within segments.
| Metapath | Classification | Segments |
|---|---|---|
| CbGiGbC | BAAB | CbG; GiG; GbC |
| DaGaDaG | BABA | DaG; GaD; DaG |
| DlAeGaDaG | BABA | DlAeG; GaD; DaG |
| CrCrC | short_repeat | CrCrC |
| DlAeG | no_repeats | DlAeG |
| CrCrCrC | long_repeat | CrCrCrC |
| CbGiGiGaDrDpCpD | interior_complete_group | CbG; GiGiG; GaD; DrD; DpC; CpD |
See Figure 3 for a breakdown of all the metapaths according to their categorization.
Figure 3: 1170 metapaths by categorization
Once the metapath is split into segments, the original metapath classification is used to select the appropriate DWPC function. For example, if the metapath classification is BAAB, then the segmented metapath will be given to the function dwpc_baab.
Each DWPC function has a unique method for ensuring that it outputs a path-count rather than a walk count. For many metapaths this was a non-trivial method to unravel, and often involved several steps of additions, subtractions, multiplications, and normalizations. Our work was greatly aided by the help of the mathematician Dr. Kyle Kloster, with whom we collaborated on some of the more challenging linear algebra algorithms.
In addition to the specific DWPC functions, I created a general method which works over all metapaths, no matter the length. While slower than the other methods, this function allows us to ensure that every path is covered by the DWPC. The method uses a dictionary of history vectors for every index in the matrix and splits computations whenever a path has the opportunity to diverge into multiple potential paths.
Our new matrix method for calculating DWPC decreased the computation time by 98.5 percent. We reduced the time to compute DWPC over nearly 1200 metepaths from roughly four-and-a-half days to roughly one hour and thirty-seven minutes [23]. One of the major advances we made in our method this summer was the realization that we can calculate the DWPC more efficiently by categorizing each metapath and feeding it to a DWPC function corresponding to a particular metapath category. These specialized functions allow us to increase significantly the speed with which we can make calculations. However, while we were able to reduce almost all computation times, there are a number of metapaths which we cannot calculate significantly more quickly than we could with the old method. 36 of 1206 metapaths had to use the generalized function I wrote which enumerates each path independently using a dictionary of history vectors in order to ensure no nodes are repeated.
For the remaining 1170 metapaths, the corresponding DWPC calculation times are summarized in Figure 4.
Figure 4: Matrix method DWPC calculation times for each of 1170 metapaths
As mentioned, we created a new system whereby metapaths are categorized according to the method we use for computing the DWPC. For example, the metapath ‘CbGbCbGaD’ is classified as BABA, due to the overlapping repeat nature of the metanodes for ‘Compound’ and ‘Gene’. See Figure 3 for a breakdown of all the metapaths according to their categorization.
In trying to reduce runtime, we were constantly trying to optimize every step in our computation. We were able to reduce runtimes significantly using sparse matrices as previously mentioned. The key, however, to a faster computational pipeline was categorizing metapaths and using specialized functions for each metapath. A breakdown of these functions’ performance is in Figure 5.
Figure 5: DWPC calculation runtimes by metapath category and path length. In this context, path length indicates the number of edges in the path.
Finally, in tracing back the slowest calculations, we found that a few metapaths took significantly longer than all others. We discovered that these involved the metapaths with the segment ‘[…]GeAeG[…]’ (see Figure 6).
Figure 6: Breakdown of the slowest metapath computation time by repeated Gene segment. ‘G_X_G’ is all metapaths which include a segment of three metanodes, whose innermost metanode is not ‘Anatomy’. ‘G_A_G’ is all metapaths with a segment ‘Gene’-‘Anatomy’-‘Gene’ except those of the form ‘GeAeG’. ‘GeAeG’ is strictly metapaths with the segment corresponding to ‘Gene-expressed-Anatomy-expressed-Gene’, meaning that there are two genes expressed in a certain anatomical region. Please note that there is no overlap between any of the three groups. ‘GeAeG’ is the most specific, and the other two groups do not include it. ‘G_X_G’ includes neither any of the ‘G_A_G’ nor of the ‘GeAeG’ metapaths.
As with many graph traversal tasks, using adjacency matrices to calculated DWPC meant that querying a set of nodes has become simpler. Our initial work has been on metapaths starting with compounds and ending with diseases. Having cached our DWPC matrices along every ‘C-[…]-D’ metapath with five or fewer edges, we can extract path counts for multiple queried nodes simply by performing matrix-vector multiplication.
I also gained a deeper appreciation of and respect for open-access and collaborative science. In working towards this, I reported a relevant bug in the open source Python repository SciPy which dealt with issues involving matrix multiplication [24].
In the deep learning review paper, I contributed a section on deep learning applications in the field of protein-protein interaction predictions, with a subsection on deep learning methods for the prediction of MHC-peptide binding [25].
We plan to use the functionality created this summer to predict potential targets for drug repurposing. By doing this, we can provide further verification for our path-count method in the same way we did for the original study. Additionally, we can verify the accuracy of our new matrix-formulation by comparing it to the far slower but precise graph method. Yet another method for verifying the predictions of our method involves comparing our predictions to new drugs which are entering the later phases of clinical trial. As these compounds are not in our Hetnet, we would hope to see that later-phase clinical trial drugs score highly in our treatment predictions for their target diseases. Luckily, a description of all such clinical trials– both active and complete in 195 countries– is available on a government website [26] run by the National Institutes of Health and the National Library of Medicine.
Now that our methods for traversing the graph are much faster and more expanded, we can add significantly more data into our heterogeneous network. A project is already underway in our lab which hopes to incorporate data mined from biomedical literature through natural language processing into our network. This project is a natural complement to the work I did this summer, because while a bigger graph requires more computation time, the matrix-based DWPC method will scale far better to increased data size than the conventional graph method.
Another use-case for our faster computation method is an increase in considered metapaths. In previous work, we have considered only a subset of the potential metapaths. For one, we only investigated metapaths starting with a compound and ending with a disease. Further, even within compound-disease metapaths, we did not consider all possible paths. Path lengths were constrained to be of length four or fewer edges in the previous work. My work this summer allows us to expand the reach of potential metapaths we consider without sacrificing hugely on performance.
As with many of the open-source projects in the Greene Lab, we hope to eventually create an open-access webserver which can access the results of our method. It should allow a user to search for as many nodes as desired and be returned a set of possible connections between them with corresponding metapaths. If this could be done, the functionality could be expanded to automatically generate a Neo4j query which could show the graphs being described by our predictions.
A final potential step forward involves extracting different features from the graph in order to make predictions about potential connections. Our method utilizes path count which corrects for degree-weight, and it has shown good performance toward predicting targets for drug repurposing. Other measures of connectedness within a graph, or other methods for degree correction could show equal or better performance, though. For example, graph centrality is a measure of the importance of certain vertices in a graph. There are feasible methods which could, for example, correct for graph centrality instead of degree for every node in a path. Even more distant from our current method is one which could incorporate some of the most exciting advances in computer science and statistics like deep learning. In such a method, we would feed a model a large amount of information about each node, and then computationally extract features without human selection. For example, in predicting protein-protein interactions, Du et al. [27] used a two-stage deep neural network first to learn the features of individual proteins which are important for predicting their interactions and second to learn the higher-level features of two proteins’ pre-selected features which predict their binding. The best way to test other methods is to split our data into training, validation, and test sets and compare the performance of different methods. In short, there are many additional methods we could employ to make predictions of future graph connections.
This summer I worked in the Greene Lab on implementing a new method for predicting drugs which could be repurposed. I contributed to this goal through several means, including the implementing a new matrix formulation of a graph node connectedness measure called the degree-weighted path count (DWPC). This measure and its new calculation method allows us to make significantly faster (66.8-fold decrease in time) calculations, whose outputs can be used to accurately predict future connections in a graph. In trying to predict compound-disease connections, our work represents a methodological advance from the previously serendipitous nature of discovering drug repurposing targets. I found this summer extremely valuable for this reason, as well as for my personal development. My computational skills have improved considerably, and my depth of understanding in the field of computational biomedical science has grown. We hope that our new method will prove useful to future researchers hoping to quickly and cheaply bring effective drugs to market, and I hope that the skills I gained this summer will be beneficial in a future biomedical research capacity.
Vagelos Scholars Program in Molecular Life Science (MLS)
Greene Lab (http://www.greenelab.com/)
Daniel Himmelstein - Postdoctoral Fellow, Greene Lab
Casey Greene - PI, Greene Lab
Kyle Kloster - Postdoctoral Researcher, North Carolina State University (NCSU)
Michael Mayers - Graduate Student, Scripps Research Institute
1. Scannell JW, Blanckley A, Boldon H, Warrington B. 2012 Diagnosing the decline in pharmaceutical R&D efficiency. Nat Rev Drug Discov 11, 191–200. See https://doi.org/10.1038/nrd3681.
2. DiMasi JA, Grabowski HG, Hansen RW. 2016 Innovation in the pharmaceutical industry: New estimates of R&D costs. Journal of Health Economics 47, 20–33. See https://doi.org/10.1016/j.jhealeco.2016.01.012.
3. DiMasi JA, Hansen RW, Grabowski HG. 2003 The price of innovation: new estimates of drug development costs. Journal of Health Economics 22, 151–185. See https://doi.org/10.1016/s0167-6296(02)00126-1.
4. DiMasi JA, Hansen RW, Grabowski HG, Lasagna L. 1991 Cost of innovation in the pharmaceutical industry. Journal of Health Economics 10, 107–142. See https://doi.org/10.1016/0167-6296(91)90001-4.
5. Pammolli F, Magazzini L, Riccaboni M. 2011 The productivity crisis in pharmaceutical R&D. Nat Rev Drug Discov 10, 428–438. See https://doi.org/10.1038/nrd3405.
6. Schuhmacher A, Gassmann O, Hinder M. 2016 Changing R&D models in research-based pharmaceutical companies. J Transl Med 14, 105. See https://www.ncbi.nlm.nih.gov/pubmed/27118048.
7. Hay M, Thomas DW, Craighead JL, Economides C, Rosenthal J. 2014 Clinical development success rates for investigational drugs. Nat Biotechnol 32, 40–51. See https://doi.org/10.1038/nbt.2786.
8. Nosengo N. 2016 Can you teach old drugs new tricks? Nature 534, 314–316. See https://doi.org/10.1038/534314a.
9. greenelab. In press. greenelab/hetmech. GitHub. See https://github.com/greenelab/hetmech.
10. greenelab. In press. greenelab/deep-review. GitHub. See https://github.com/greenelab/deep-review.
11. Himmelstein DS, Lizee A, Hessler C, Brueggeman L, Chen SL, Hadley D, Green A, Khankhanian P, Baranzini SE. 2016 Systematic integration of biomedical knowledge prioritizes drugs for repurposing. See https://doi.org/10.1101/087619.
12. Weisstein EW. In press. Adjacency Matrix. MathWorld–A Wolfram Web Resource. See http://mathworld.wolfram.com/AdjacencyMatrix.html.
13. Himmelstein DS, Baranzini SE. 2015 Heterogeneous Network Edge Prediction: A Data Integration Approach to Prioritize Disease-Associated Genes. PLoS Comput Biol 11, e1004259. See https://doi.org/10.1371/journal.pcbi.1004259.
14. numpy. In press. numpy/numpy. GitHub. See https://github.com/numpy/numpy.
15. scipy. In press. scipy/scipy. GitHub. See https://github.com/scipy/scipy.
16. jupyter. In press. jupyter/notebook. GitHub. See https://github.com/jupyter/notebook.
17. pandas-dev. In press. pandas-dev/pandas. GitHub. See https://github.com/pandas-dev/pandas.
18. 2017 17.4. concurrent.futures — Launching parallel tasks — Python 3.6.2 documentation. See https://docs.python.org/3/library/concurrent.futures.html.
19. Technology N. 2017 Hetionet · Neo4j Browser. See https://neo4j.het.io/browser/.
20. matplotlib. In press. matplotlib/matplotlib. GitHub. See https://github.com/matplotlib/matplotlib.
21. 2017 seaborn: statistical data visualization — seaborn 0.8.0 documentation. See https://seaborn.pydata.org/.
22. In press. Greene Laboratory. GitHub. See https://github.com/greenelab.
23. dhimmel. In press. dhimmel/learn. GitHub. See https://github.com/dhimmel/learn/blob/master/all-features/3-extract.ipynb.
24. scipy. In press. Operations between numpy.array and scipy.sparse matrix return inconsistent array type · Issue #7510 · scipy/scipy. GitHub. See https://github.com/scipy/scipy/issues/7510.
25. greenelab. In press. Added PPI section with MHC subsection by zietzm · Pull Request #638 · greenelab/deep-review. GitHub. See https://github.com/greenelab/deep-review/pull/638.
26. In press. Home - ClinicalTrials.gov. See https://clinicaltrials.gov/.
27. Du X, Sun S, Hu C, Yao Y, Yan Y, Zhang Y. 2017 DeepPPI: Boosting Prediction of Protein–Protein Interactions with Deep Neural Networks. J. Chem. Inf. Model. 57, 1499–1510. See https://doi.org/10.1021/acs.jcim.7b00028.